다른 틀로부터 틀의 상대적인 방향을 표현하기 위해 다음과 같은 3-벡터 사용
이러한 표현 방법을 Exponential Coordinate for Rotations 라고 하며, 이는 회전 행렬을 표현하는 또다른 방법
이때, w는 각속도로써 이를 적분하면 초기 orientation으로부터 최종 orientation을 찾아낼 수 있음

w를 적분하기 위해서는 선형 미분 방적식을 풀어야 함 (Linear Differential Equations Problem)
a가 스칼라가 아닌 벡터 A로 표현될 수도 있는데, 이때의 e^At 를 matrix exponential 이라고 함

지수 함수는 다음과 같이 series expension 방법으로 표현할 수도 있음

행렬 지수는 rigid body의 rotation을 구하는데 사용됨

회전축 w에 따라 p가 회전하는 경우, p의 속도는 다음과 같이 나타냄
w가 A처럼 작용하기 때문에, p의 속도는 행이 3개인 열벡터가 됨

그리고 이를 skew-symmetrix matrix를 사용하여 표현하면 다음과 같음
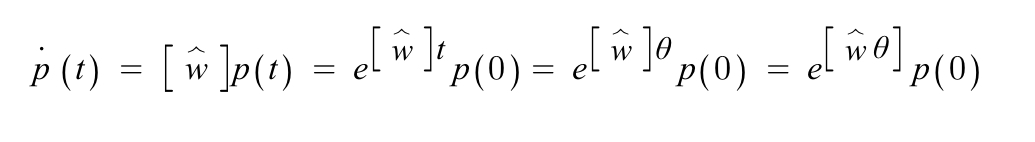
일반적으로 행렬 지수를 풀어낼 땐 series expension 방법 사용
그러나 3x3의 skew-symmetrix matrix인 경우 다음과 같이 간단한 closed form으로 표현 가능
이 closed firm을 Rodrigues' formula 라고 함

예를 들어
axis w(0, 0.966, 0.5)
θ = 0.524 rad
Rodrigues' formula 를 이용하여 frame {b}의 rotation matrix를 구할 수 있음

반대로 미분의 형태로 Rotation을 이용해 각속도를 구할 수도 있음
